Looking Ahead (and Behind)

• Week 4: Correlation

• Last week: Chi-Square ( ${\chi }^2$ )

• This week: t-test

• Next week: The Linear Model

• Week 8: The Linear Model

Lab Report: Red Study

• Today we will talk about one of the analyses for the lab report

  • ${\chi }^2$ : Green study (Griskevicious et al., 2010), last week

  • t-test: Red study (Elliot et al., 2020), today!

• We will talk about the lab report in the lectures and work on it in the practicals

  • Make sure you come to your registered sessions

Objectives

After this lecture you will understand:

• The concepts behind comparing two means

  • Independent and paired samples t-tests

• Where the t-statistic comes from

• How to read histograms and means plots

• How to interpret and report significance tests of t

Comparing Two Means

• Extremely common and fundamental testing paradigm

• Comparing means in two groups

  • Independent: different entities/participants in each groups

  • Paired: same entities/participants in both groups

• Very similar logic and interpretation, slightly different maths!

Taste the Rainbow: Synaesthesia Again

• People with synaesthesia have unusual sensory experiences

  • Experience colours for words, shapes for music, personalities for numbers, etc.

Grapheme-Colour Synaesthesia

• Association between letters/words and particular colours

  • Tends to be consistent throughout life, beginning in childhood

  • So, synaesthetes might tend to notice language/spelling more often

• Research question: Do synaesthetes have a particular cognitive style, compared to non-synaesthetes?

• Conceptual hypothesis: grapheme-colour synaesthetes have a more language-oriented cognitive style than non-synaesthetes

Data and Design: SCSQ

• Mealor et al (2016): Sussex Cognitive Styles Questionnaire

  • Includes measures of imagery, language ability, and more

  • Validated on people with and without synaesthesia

• Operational hypothesis: Synaesthetes will, on average, have a different score on the Language subscale of the SCSQ than non-synaesthetes

  • Example items: "I tend to notice if a word has the same letter repeated in its spelling"; "I enjoy learning new languages"

• Null hypothesis: Synaesthetes and non-synaesthetes will, on average, have the same score on the Language subscale

Having a Look

• All scores on the Language subscale together

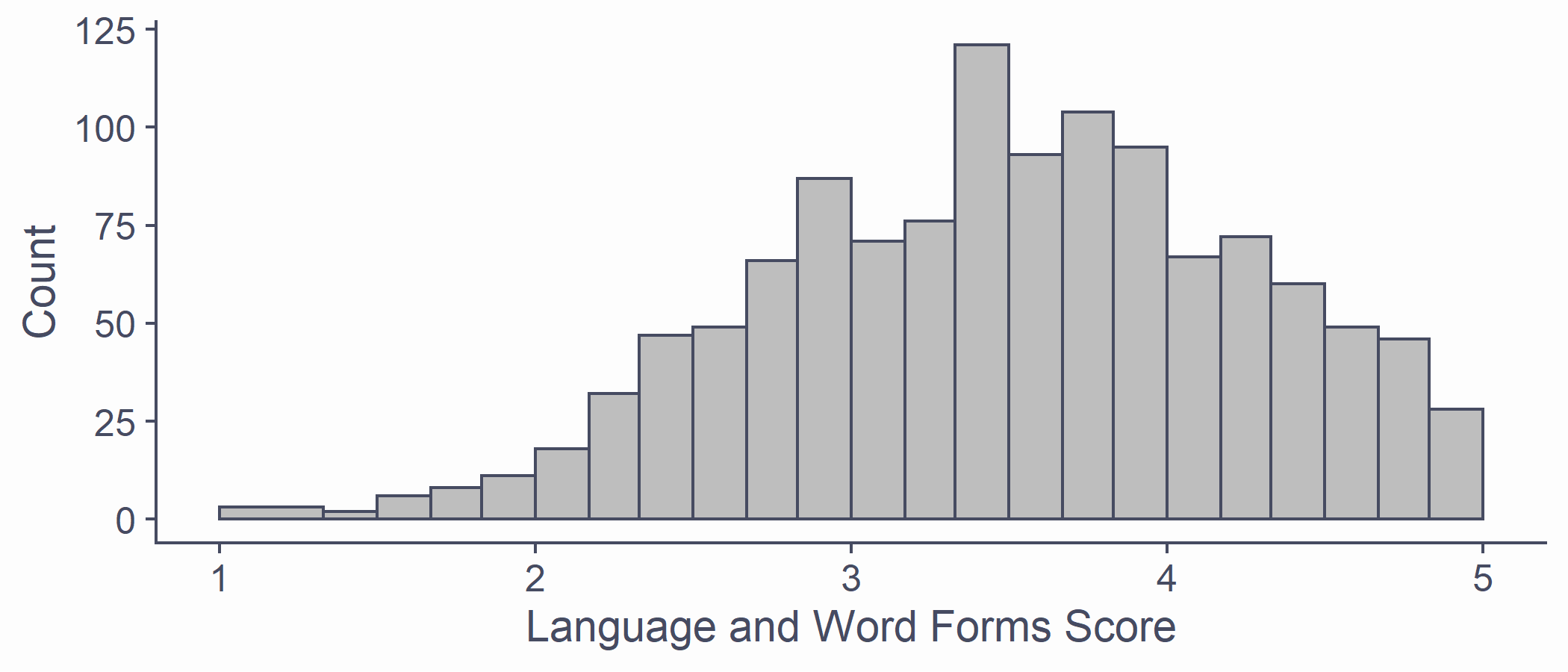
syn_data %>% 
  ggplot(aes(x = Language)) +
  geom_histogram(breaks = syn_data %>% pull(Language) %>% unique(), fill = "grey") +
  scale_x_continuous(name = "Language and Word Forms Score",
                     limits = c(1, 5)) +
  scale_y_continuous(name = "Count")

Having a Look

• Split up by grapheme-colour synaesthesia

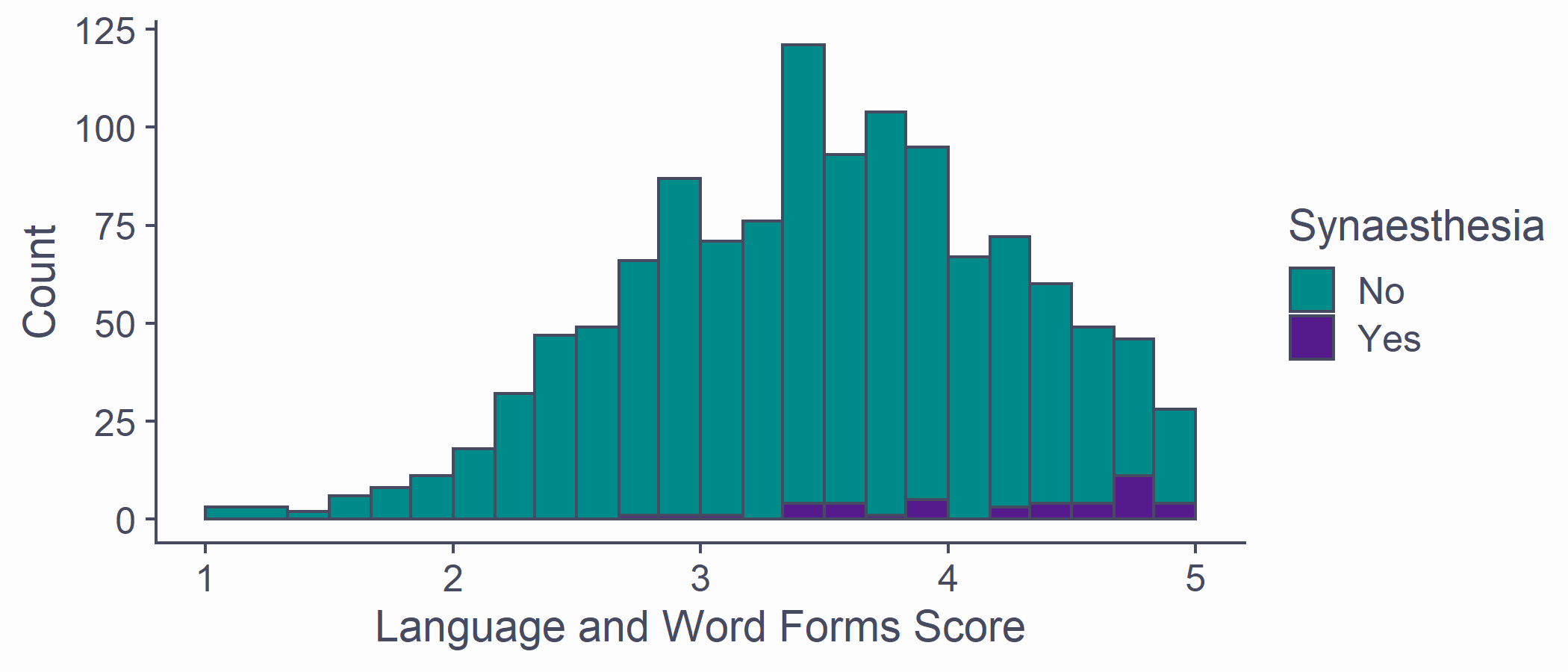
syn_data %>% 
  ggplot(aes(x = Language, fill = GraphCol)) +
  geom_histogram(breaks = syn_data %>% pull(Language) %>% unique()) +
  scale_x_continuous(name = "Language and Word Forms Score",
                     limits = c(1, 5)) +
  scale_y_continuous(name = "Count") +
  scale_fill_discrete(name = "Synaesthesia",
                      type = c("darkcyan", "purple4"))

Having a Look

• Dotted lines for mean scores in each group

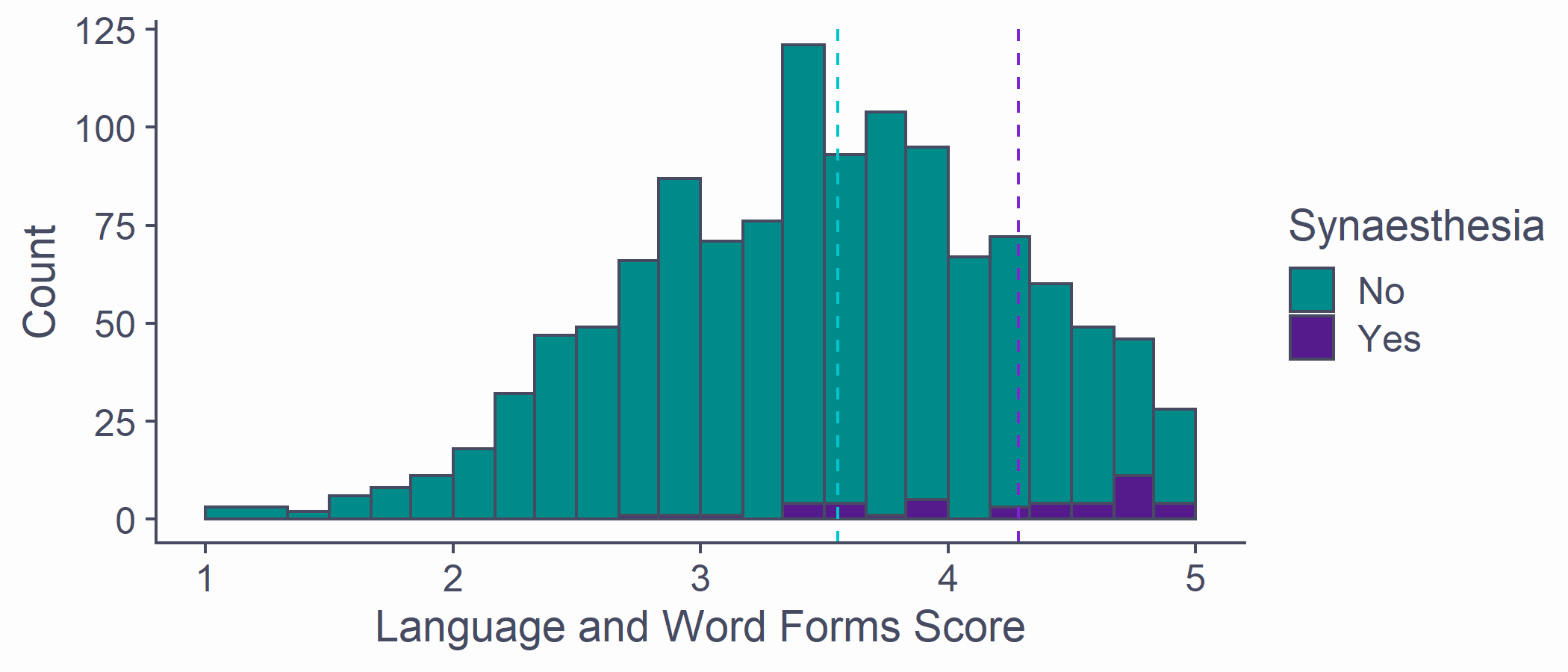
syn_data %>% 
  ggplot(aes(x = Language, fill = GraphCol)) +
  geom_histogram(breaks = syn_data %>% pull(Language) %>% unique()) +
  scale_x_continuous(name = "Language and Word Forms Score",
                     limits = c(1, 5)) +
  scale_y_continuous(name = "Count") +
  scale_fill_discrete(name = "Synaesthesia",
                      type = c("darkcyan", "purple4")) +
  geom_vline(aes(xintercept = mean(Language)), 
             data = syn_data %>% filter(GraphCol == "Yes"),
             colour = "purple3",
             linetype = "dashed") +
  geom_vline(aes(xintercept = mean(Language)), 
             data = syn_data %>% filter(GraphCol == "No"),
             colour = "turquoise3",
             linetype = "dashed")

Sorted!

• The mean Language score for synaesthetes is higher than for non-synaesthetes

• Are we done?

• Of course not 😉

• How different are these mean scores, accounting for the variation in scores?

  • How strong is the signal (the difference in means)...

  • Compared to the noise (the variation in scores around the mean)?

Having a Closer Look

• Plot of the means in each group

  • Error bars represent 2 $\times$ the standard error

• How can we interpret this plot?

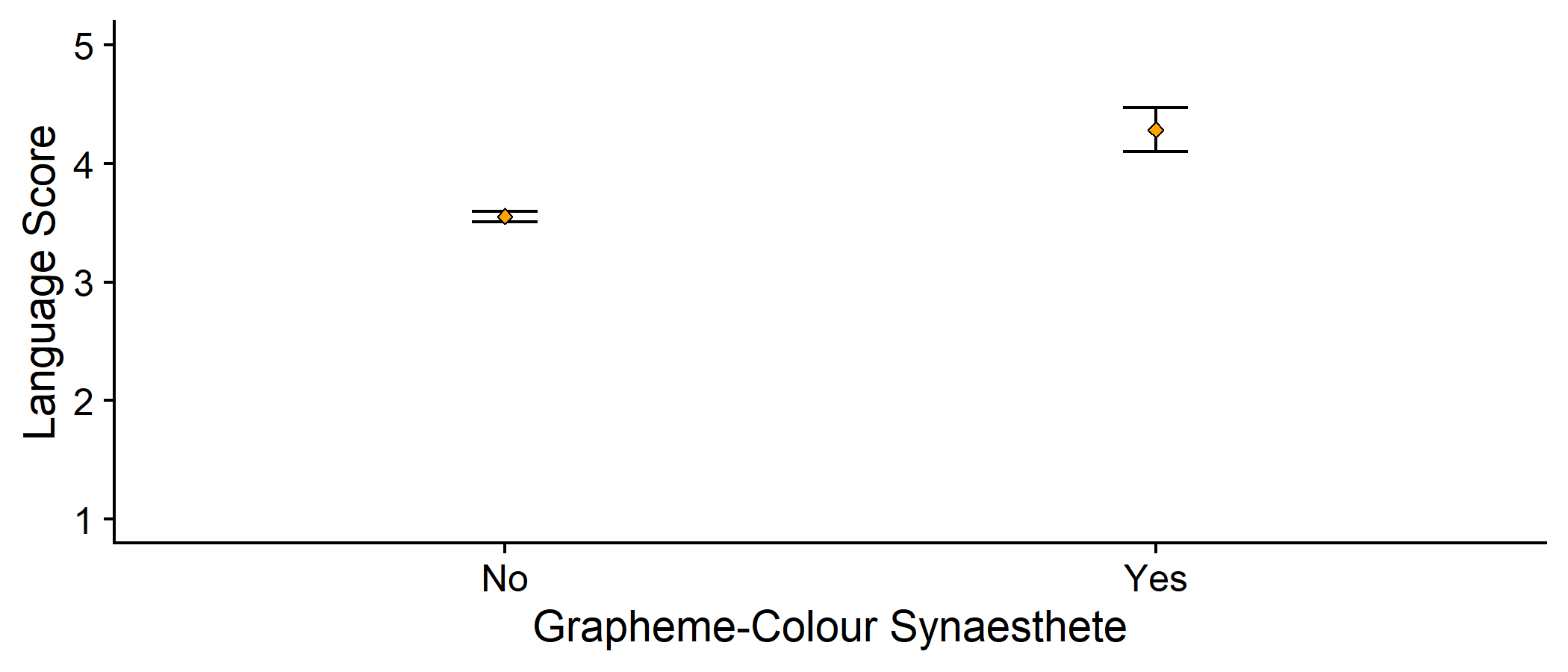
syn_data %>% 
  dplyr::group_by(GraphCol) %>% 
  dplyr::summarise(
    n = dplyr::n(),
    mean_lang = mean(Language),
    se_lang = sd(Language)/sqrt(n)
  ) %>% 
  ggplot2::ggplot(aes(x = GraphCol, y = mean_lang)) +
  geom_errorbar(aes(ymin = mean_lang - 2*se_lang, ymax = mean_lang + 2*se_lang), width = .1) +
  geom_point(colour = "black", fill = "orange", pch = 23) +
  scale_y_continuous(name = "Language Score",
                     limits = c(1, 5)) +
  labs(x = "Grapheme-Colour Synaesthete") +
  cowplot::theme_cowplot()

Why You Gotta Be So Mean

• Let's get some numbers to work with 😁

  • Mean in synaesthete group: 4.29

  • Mean in nonsynaesthete group: 3.55

  • Difference in the means = 4.29 - 3.55 = 0.74

• Is this a big difference, compared to how different we might expect for any two sample means from the same population?

Steps of the Analysis

• Calculate the (standardised) difference between mean scores

• Compare that test statistic to its distribution under the null hypothesis

• Obtain the probability p of encountering a test statistic of the size we have, or larger, if the null hypothesis is true

## 
##     Two Sample t-test
## 
## data:  Language by GraphCol
## t = -6.3394, df = 1209, p-value = 0.000000000325
## alternative hypothesis: true difference in means is not equal to 0
## 95 percent confidence interval:
##  -0.9576637 -0.5049972
## sample estimates:
##  mean in group No mean in group Yes 
##          3.554949          4.286279

• Where does this number t come from? And what does it mean?

Let's Think About This

• Imagine we took two samples of scores from a single population and calculated their means, and then found the difference between those means

• Create a sampling distribution of mean differences

  • Centre of the distribution = 0 (no difference between the means)

  • Very small differences in means will be quite common

  • Very large differences in means will be quite unlikely

• Distribution under the null hypothesis that which group you're in (e.g. synaesthete vs non-synaesthete) makes no difference to your score

  • Samples come from the same population of scores

Sound Familiar?

• If this rings a bell, it should!

  • This is the same scenario from Lecture 3 for the Ape Index (AI)

Sound Familiar?

• Our estimate of mean Language score difference (0.74) also has some distribution

  • Using that distribution, obtain the probability p of finding a difference as large as the one we found, or larger, if the null hypothesis is true (as usual)

• Standardise our mean difference to compare it to a known distribution

  • We can do this by dividing the mean difference by the standard error

  • In other words: scale it to the distribution

  • Conceptually similar to z-scores

Same But Different

• For the AI in Lecture 3, the standard deviation of the population was 1

  • Assumed for simplicity

  • Remember, $SE=\frac{\sigma }{\sqrt{n}}$

• For our synaesthesia example, the standard error is a variable

  • We estimate $\widehat{SE}$ based on the standard deviation s

  • Every sample, even samples of the same size, will have a different s!

What's the Point?

• The test statistic t is the difference in group means divided by the standard error

  • Difference in group means: the effect of interest, or signal

  • Standard error of the difference in means: the error, or noise

• So, t represents how big the signal is compared to the noise

  • Larger values of t are more unlikely under the null hypothesis (when the "signal" is really 0!)

Would You Like Some t?

• Naturally, t is t-distributed (here, with N₁ + N₂ - 2 degrees of freedom)

• Given an $\alpha$ level of .05...

  • If p > .05, we conclude that our results are likely to occur under the null hypothesis, so we have no evidence that the null hypothesis is not true

  • If p < .05, we conclude that our results are sufficiently unlikely to occur that it may in fact be the case that the null hypothesis is not true

Would You Like Some t?

## 
##     Two Sample t-test
## 
## data:  Language by GraphCol
## t = -6.3394, df = 1209, p-value = 0.000000000325
## alternative hypothesis: true difference in means is not equal to 0
## 95 percent confidence interval:
##  -0.9576637 -0.5049972
## sample estimates:
##  mean in group No mean in group Yes 
##          3.554949          4.286279

Interim Summary

• Independent samples t-test

  • Tests whether two different samples come from the same population using t

  • If p < $\alpha$ (typically .05), then it is unlikely that they do

  • So, we conclude that group membership is associated with some difference

• If you choose the Red study, this is the test you will use

• Next up: paired samples t-test

Do You Want Some Synaesthesia?

• Being a synaesthete is super cool and a lot of fun

  • See cool colours all the time!

  • Have (very mundane and mostly unremarkable) superpowers!

• What if everyone could be a synaesthete?

  • Can you train people to have synaesthesia?

Paired (Repeated) Design

• Simplified version of Bor et al. (2014)

• Train people to associate colours with letters

• Test success of the training with a modified Stroop task

  • Outcome: naming speed pre- vs post-training

Paired (Repeated) Design

• Key difference: the same people participate in both conditions

## # A tibble: 6 x 2
##     pre  post
##   <dbl> <dbl>
## 1  842.  780.
## 2  688.  633.
## 3  682.  626.
## 4  697.  637.
## 5  278.  219.
## 6  646.  588.

Example Output

## 
##     Paired t-test
## 
## data:  syn_train$pre and syn_train$post
## t = 90.76, df = 13, p-value < 0.00000000000000022
## alternative hypothesis: true difference in means is not equal to 0
## 95 percent confidence interval:
##  57.03779 59.81936
## sample estimates:
## mean of the differences 
##                58.42857

Causality

• In our first example, could we conclude that having synaesthesia causes you to pay more attention to language?

• In our second example, could we conclude that having training causes you to associate colours with letters?

• Why is this?

That's the t

• The t-test quantifies the size of the difference of two means (signal) compared to the error (noise)

• Independent samples t-test

  • Tests means from different entities/participants

  • Independent or "between-subjects" design

• Paired samples t-test

  • Tests means from the same entities/participants

  • Repeated or "within-subjects" design

• Establishing causality is a function of study design not statistics!

Lab Reports

• You can choose either the red or green study to write your report on

  • See Lab Report Information on Canvas for more

• If you choose the red study (Elliot et al., 2010), you must use and report the results of an independent samples t-test

• Create a composite score out of the three rating scales

• Report means, SDs, and t-test result

  • Include a figure of the results

  • Will be covered in depth in the next tutorial and practical!