Announcements
Lab Report Drop-ins starting next week
Next week's practicals: Writing up lab report results
Week 9 practicals will start on the Linear Model
You still have a tutorial and quiz this week!
Next week: Academic Advising session on Discussion writing
- Designed for this assessment - please attend
Awards: SavioR nominations and Education Awards
Feedback via the Suggestions Box

Objectives
After this lecture you will understand:
What a statistical model is and why they are useful
The equation for a linear model with one predictor
b0 (the intercept)
b1 (the slope)
Both categorical and continuous predictors
Using the equation to predict an outcome
How to read scatterplots and lines of best fit

The Linear Model
Extremely common and fundamental testing paradigm
Predict the outcome y from one or more predictors (xs)
Our first (explicit) contact with statistical modeling
A statistical model is a mathematical expression that captures the relationship between variables
- All of our test statistics (r, t, etc.) are actually models!

Maps as Models
A map is a simplified depiction of the world
Captures the important elements (roads, cities, oceans, mountains)
Doesn't capture individual detail (where your gran lives)
Depicts relationships between locations and geographical features
Helps you predict what you will encounter in the world
E.g. if you keep walking south eventually you'll fall in the sea!

Statistical Models
A model is a simplified depiction of some relationship
We want to predict what will happen in the world
But the world is complex and full of noise (randomness)
We can build a model to try to capture the important elements
- Change/adjust the model to see what might happen with different parameters

Predictors and Outcomes
Now we start assigning our variables roles to play
The outcome is the variable we want to explain
- Also called the dependent variable, or DV
The predictors are variables that may have a relationship with the outcome
- Also called the independent variable(s), or IV(s)
We measure or manipulate the predictors, then quantify the systematic change in the outcome
- NB: YOU (the researcher) assign these roles!

Making Predictions
Last week, we looked at the Language and Word Forms subscale of the SCSQ
If I wanted to predict someone's Language score...
- What would be the most sensible estimate?
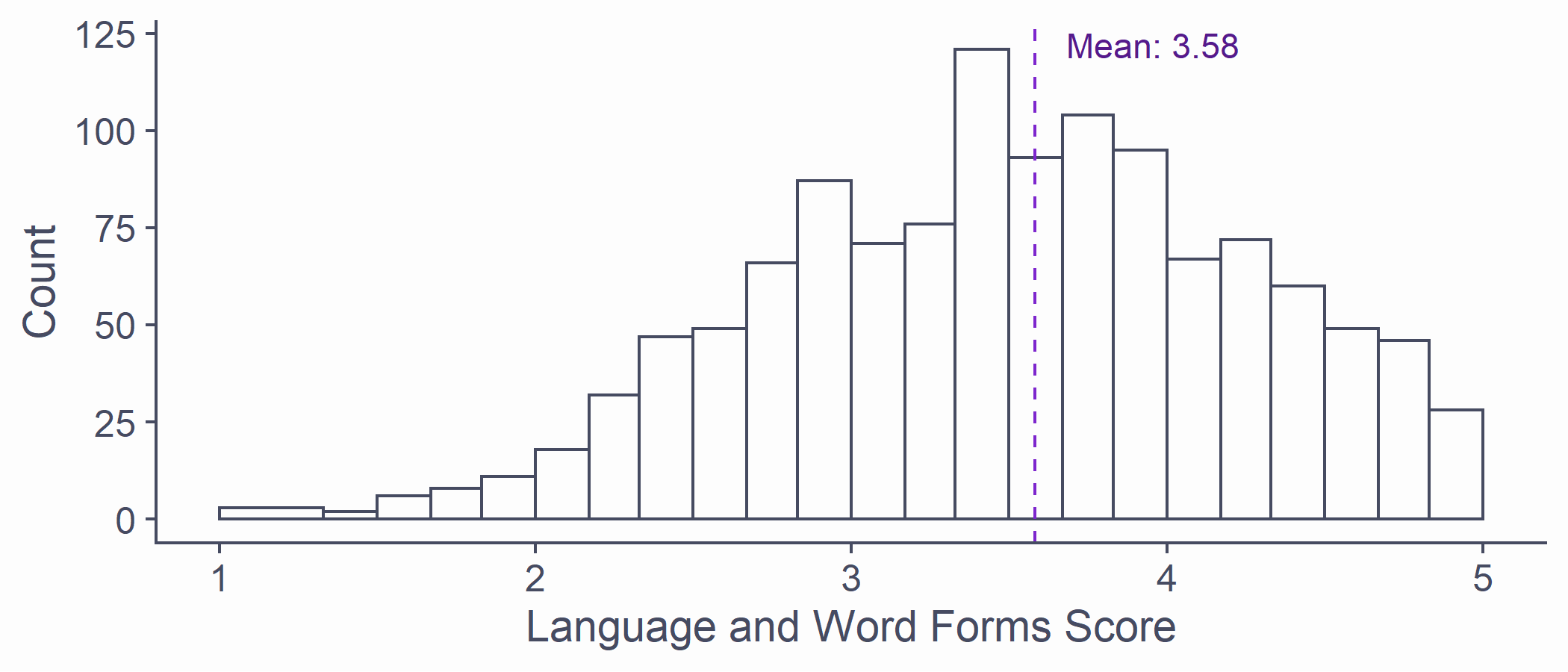
syn_data %>% ggplot(aes(x = Language)) + geom_histogram(breaks = syn_data %>% pull(Language) %>% unique()) + scale_x_continuous(name = "Language and Word Forms Score", limits = c(1, 5)) + scale_y_continuous(name = "Count") + scale_fill_discrete(name = "Synaesthesia") + geom_vline(aes(xintercept = mean(Language)), colour = "purple3", linetype = "dashed") + annotate("text", x = mean(syn_data$Language) + .1, y = 122, label = paste0("Mean: ", mean(syn_data$Language) %>% round(2)), hjust=0, colour = "purple4")
Making Predictions
Without any other information, the best estimate is the mean of the outcome
- But we do have more information!
Last week: Grapheme-colour synaesthetes score higher than non-synaesthetes on the Language subscale on average
We could make a better prediction if we knew whether that person was a synaesthete
Use the mean score in the synaesthete vs non-synaesthete groups

Making Predictions
Without any other information, the best estimate is the mean of the outcome
- But we do have more information!
Last week: Grapheme-colour synaesthetes score higher than non-synaesthetes on the Language subscale on average
We could make a better prediction if we knew whether that person was a synaesthete
Use the mean score in the synaesthete vs non-synaesthete groups
Let's write an equation that we can use to predict someone's score based on whether they are a synaesthete or not!

Making Predictions
First: the non-synaesthete (baseline) group
If someone is a non-synaesthete, predicted Language score = 3.55
^Languagenon−syn=3.55
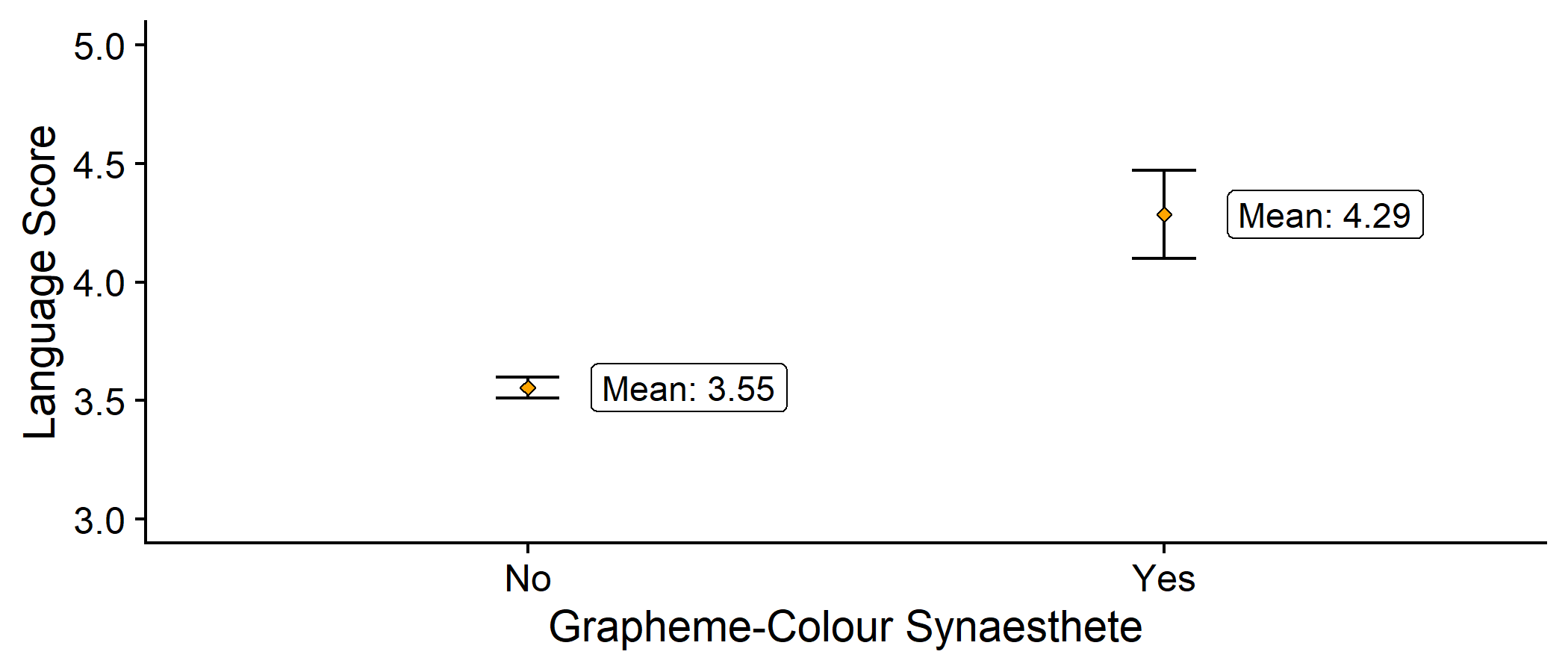
syn_data %>% dplyr::group_by(GraphCol) %>% dplyr::summarise( n = dplyr::n(), mean_lang = mean(Language), se_lang = sd(Language)/sqrt(n) ) %>% ggplot2::ggplot(aes(x = GraphCol, y = mean_lang)) + geom_errorbar(aes(ymin = mean_lang - 2*se_lang, ymax = mean_lang + 2*se_lang), width = .1) + geom_point(colour = "black", fill = "orange", pch = 23) + scale_y_continuous(name = "Language Score", limits = c(3, 5)) + labs(x = "Grapheme-Colour Synaesthete") + geom_label(stat = 'summary', fun.y=mean, aes(label = paste0("Mean: ", round(..y.., 2))), nudge_x = 0.1, hjust = 0) + cowplot::theme_cowplot()
Making Predictions
Next: the synaesthete group
If someone is a synaesthete, predicted Language score = 4.29
^Languagesyn=3.55+0.74
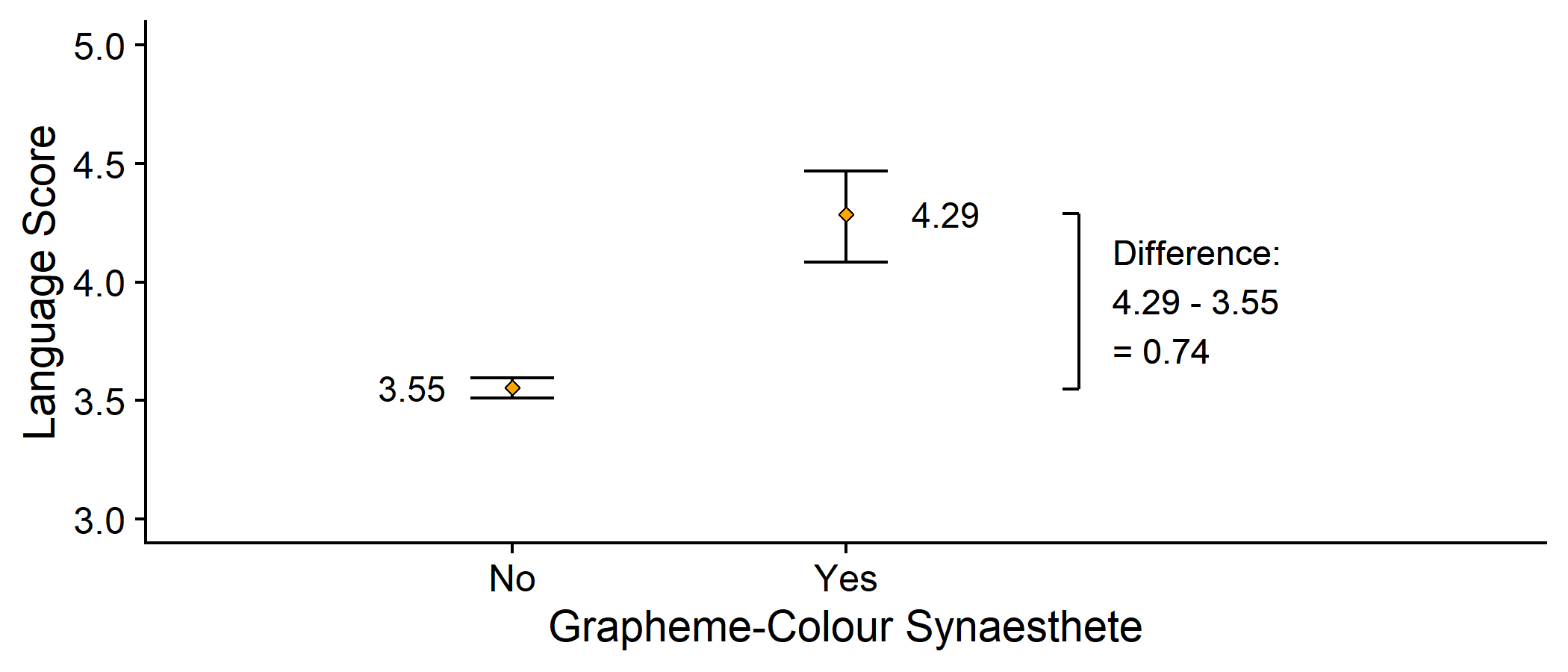
bracket <- syn_data %>% group_by(GraphCol) %>% summarise(y = mean(Language)) %>% mutate(x = rep(2.7, 2), y = round(y, 2))syn_data %>% ggplot(aes(x = GraphCol, y = Language)) + #geom_line(stat="summary", fun = mean, aes(group = NA)) + geom_errorbar(stat = "summary", fun.data = mean_cl_boot, width = .25) + geom_point(stat = "summary", fun = mean, shape = 23, fill = "orange") + geom_text(aes(label=round(..y..,2)), stat = "summary", fun = mean, size = 4, nudge_x = c(-.3, .3)) + geom_line(data = bracket, mapping = aes(x, y)) + geom_segment(data = bracket, mapping = aes(x, y, xend = x - .05, yend = y)) + annotate("text", x = bracket$x + .1, y = min(bracket$y) + diff(bracket$y)/2, label = paste0("Difference:\n", bracket$y[2], " - ", bracket$y[1], "\n= ", diff(bracket$y)), hjust=0) + coord_cartesian(xlim = c(0.5, 3.5), ylim = c(3,5)) + scale_y_continuous(name = "Language Score") + labs(x = "Grapheme-Colour Synaesthete") + cowplot::theme_cowplot()
Making Predictions
We want our equation to give a different prediction depending on whether someone is a synaesthete or not
^Language=3.55
^Languagei=3.55+0.74×GraphColi
When someone is a non-synaestheste (GraphCol = 0)...
^Languagei=3.55+0.74×0
^Languagei=3.55
When someone is a synaesthete (GraphCol = 1)...
^Languagei=3.55+0.74×1
^Languagei=3.55+0.74
^Languagei=4.29

Drawing Lines
- This equation represents a linear model (a line!) between the means
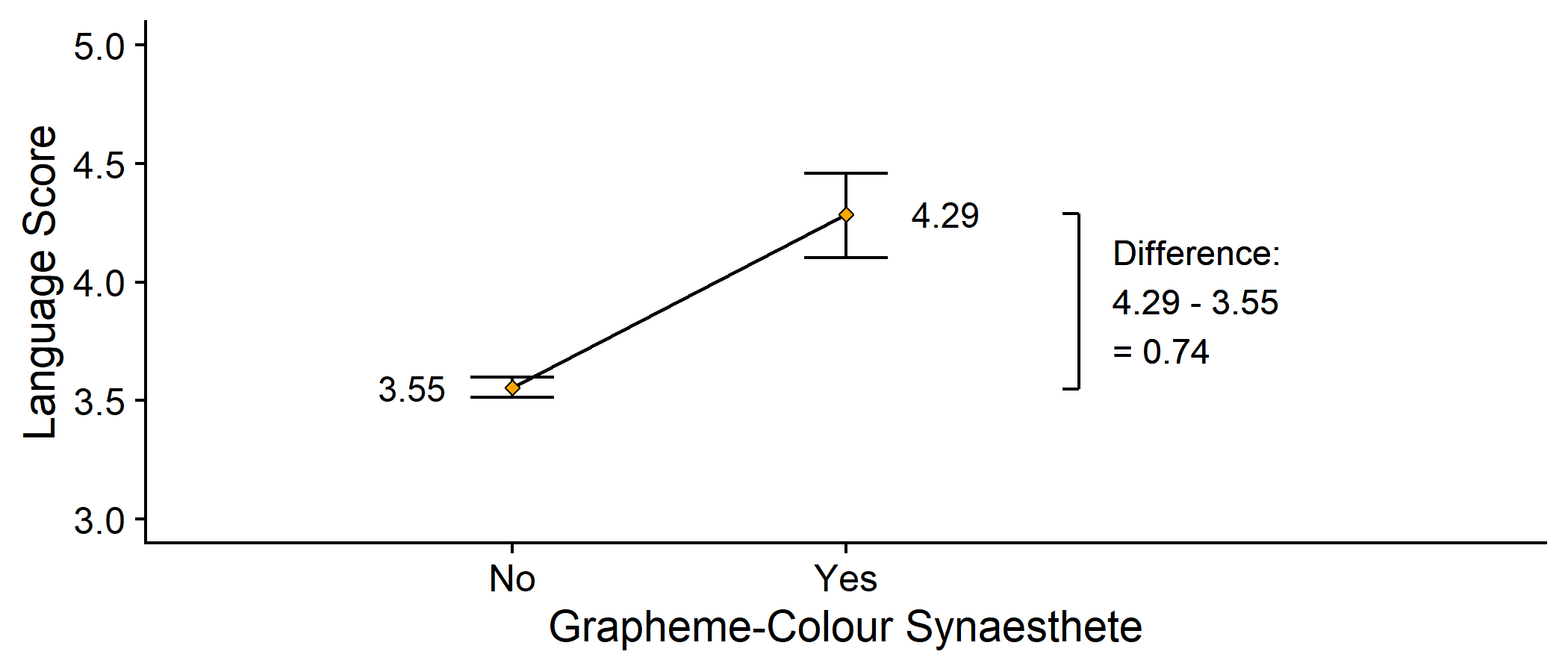
bracket <- syn_data %>% group_by(GraphCol) %>% summarise(y = mean(Language)) %>% mutate(x = rep(2.7, 2), y = round(y, 2))syn_data %>% ggplot(aes(x = GraphCol, y = Language)) + geom_line(stat="summary", fun = mean, aes(group = NA)) + geom_errorbar(stat = "summary", fun.data = mean_cl_boot, width = .25) + geom_point(stat = "summary", fun = mean, shape = 23, fill = "orange") + geom_text(aes(label=round(..y..,2)), stat = "summary", fun = mean, size = 4, nudge_x = c(-.3, .3)) + geom_line(data = bracket, mapping = aes(x, y)) + geom_segment(data = bracket, mapping = aes(x, y, xend = x - .05, yend = y)) + annotate("text", x = bracket$x + .1, y = min(bracket$y) + diff(bracket$y)/2, label = paste0("Difference:\n", bracket$y[2], " - ", bracket$y[1], "\n= ", diff(bracket$y)), hjust=0) + coord_cartesian(xlim = c(0.5, 3.5), ylim = c(3,5)) + scale_y_continuous(name = "Language Score", limits = c(1, 5)) + labs(x = "Grapheme-Colour Synaesthete") + cowplot::theme_cowplot()
Drawing Lines
The line starts from the mean of the non-synaesthete group
This is the intercept, which we will call b0
The predicted value of the outcome ^y when the predictor x is 0
Changing to the synaesthete group, predicted Language score changes by 0.74
This is the slope of the line, which we will call b1
The change in the outcome for every unit change in the predictor

Drawing Lines
The line starts from the mean of the non-synaesthete group
This is the intercept, which we will call b0
The predicted value of the outcome ^y when the predictor x is 0
Changing to the synaesthete group, predicted Language score changes by 0.74
This is the slope of the line, which we will call b1
The change in the outcome for every unit change in the predictor
- This prediction will always have some amount of error, e

Drawing Lines
The line starts from the mean of the non-synaesthete group
This is the intercept, which we will call b0
The predicted value of the outcome ^y when the predictor x is 0
Changing to the synaesthete group, predicted Language score changes by 0.74
This is the slope of the line, which we will call b1
The change in the outcome for every unit change in the predictor
This prediction will always have some amount of error, e
In general, then, the linear model has the form:
yi=b0+b1x1i+ei

Drawing Lines
## ## Call:## lm(formula = Language ~ GraphCol, data = syn_data)## ## Coefficients:## (Intercept) GraphColYes ## 3.5549 0.7313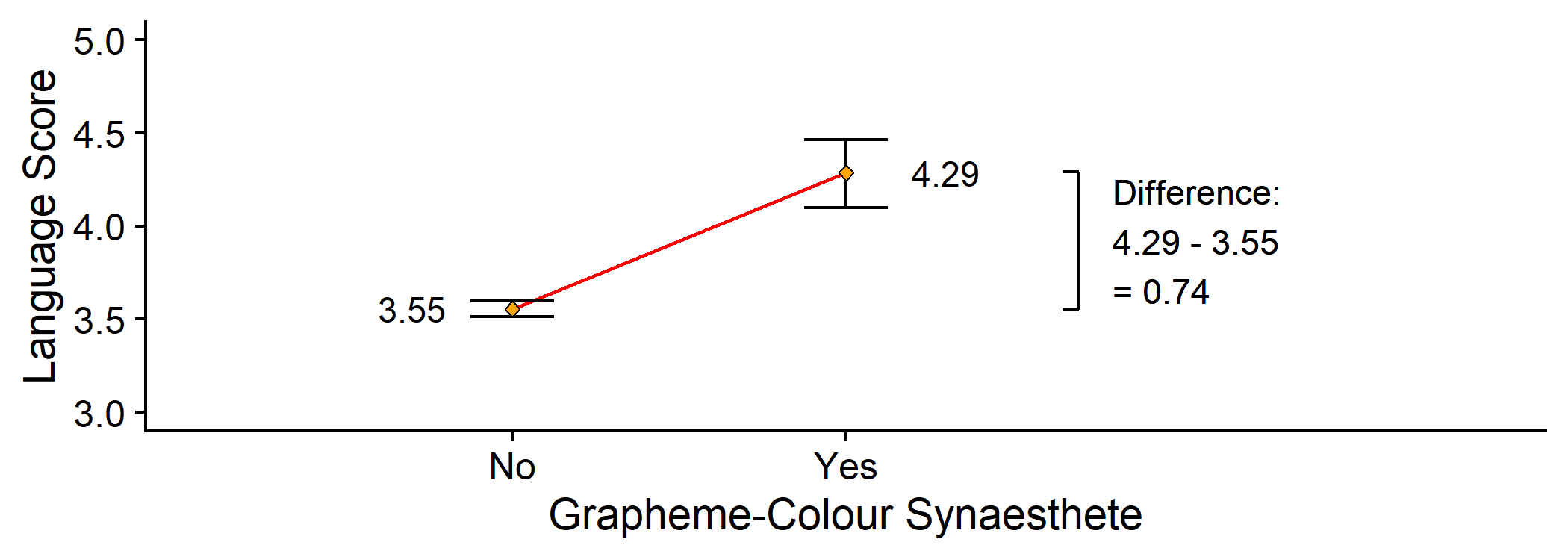
bracket <- syn_data %>% group_by(GraphCol) %>% summarise(y = mean(Language)) %>% mutate(x = rep(2.7, 2), y = round(y, 2))syn_data %>% ggplot(aes(x = GraphCol, y = Language)) + geom_line(stat="summary", fun = mean, aes(group = NA), colour = "red") + geom_errorbar(stat = "summary", fun.data = mean_cl_boot, width = .25) + geom_point(stat = "summary", fun = mean, shape = 23, fill = "orange") + geom_text(aes(label=round(..y..,2)), stat = "summary", fun = mean, size = 4, nudge_x = c(-.3, .3)) + geom_line(data = bracket, mapping = aes(x, y)) + geom_segment(data = bracket, mapping = aes(x, y, xend = x - .05, yend = y)) + annotate("text", x = bracket$x + .1, y = min(bracket$y) + diff(bracket$y)/2, label = paste0("Difference:\n", bracket$y[2], " - ", bracket$y[1], "\n= ", diff(bracket$y)), hjust=0) + coord_cartesian(xlim = c(0.5, 3.5), ylim = c(3,5)) + scale_y_continuous(name = "Language Score", limits = c(1, 5)) + labs(x = "Grapheme-Colour Synaesthete") + cowplot::theme_cowplot()
Making Connections
Remember from last week: the "signal" of interest was the difference in means
That same value (0.74) is also the value of b1! (ignoring rounding error...)
The change in Language between synaesthetes and non-synaesthetes
Quantifies the relationship between the predictor and the outcome
This is the key element of the linear model!

Interim Summary
The linear model predicts the outcome y based on a predictor x
General form: yi=b0+b1x1i+ei
b0: the intercept, or value of y when x is 0
b1: the slope, or change in y for every unit change in x
The slope b1 represents the relationship between the predictor and the outcome
Up next: continuous predictors

Visualising the Line
- Ratings of femininity vs masculinity
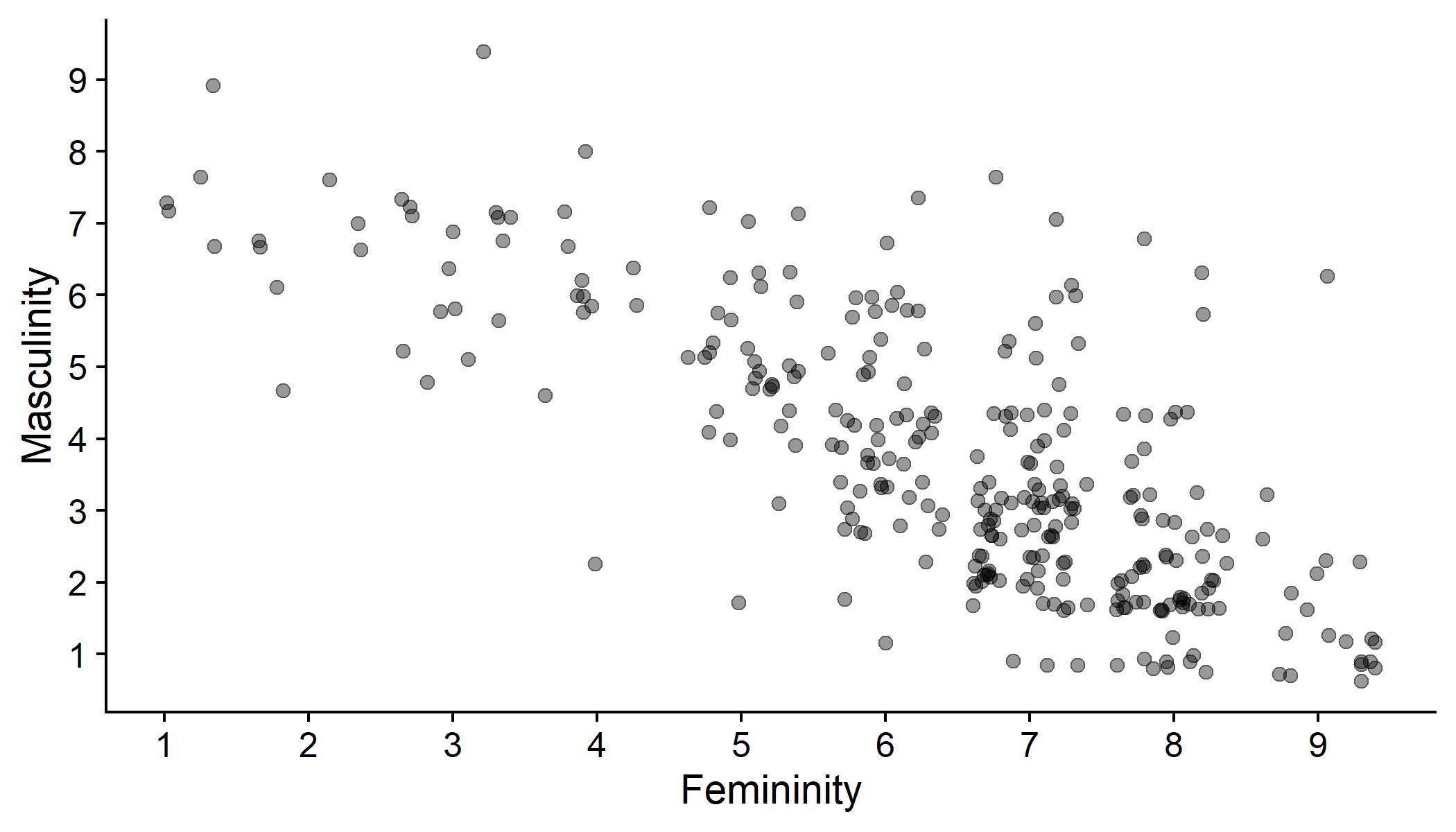
gensex %>% mutate(Gender = fct_explicit_na(Gender)) %>% ggplot(aes(x = Gender_fem_1, y = Gender_masc_1)) + geom_point(position = "jitter", size = 2, alpha = .4) + scale_x_continuous(name = "Femininity", breaks = c(0:9)) + scale_y_continuous(name = "Masculinity", breaks = c(0:9)) + cowplot::theme_cowplot()
Visualising the Line
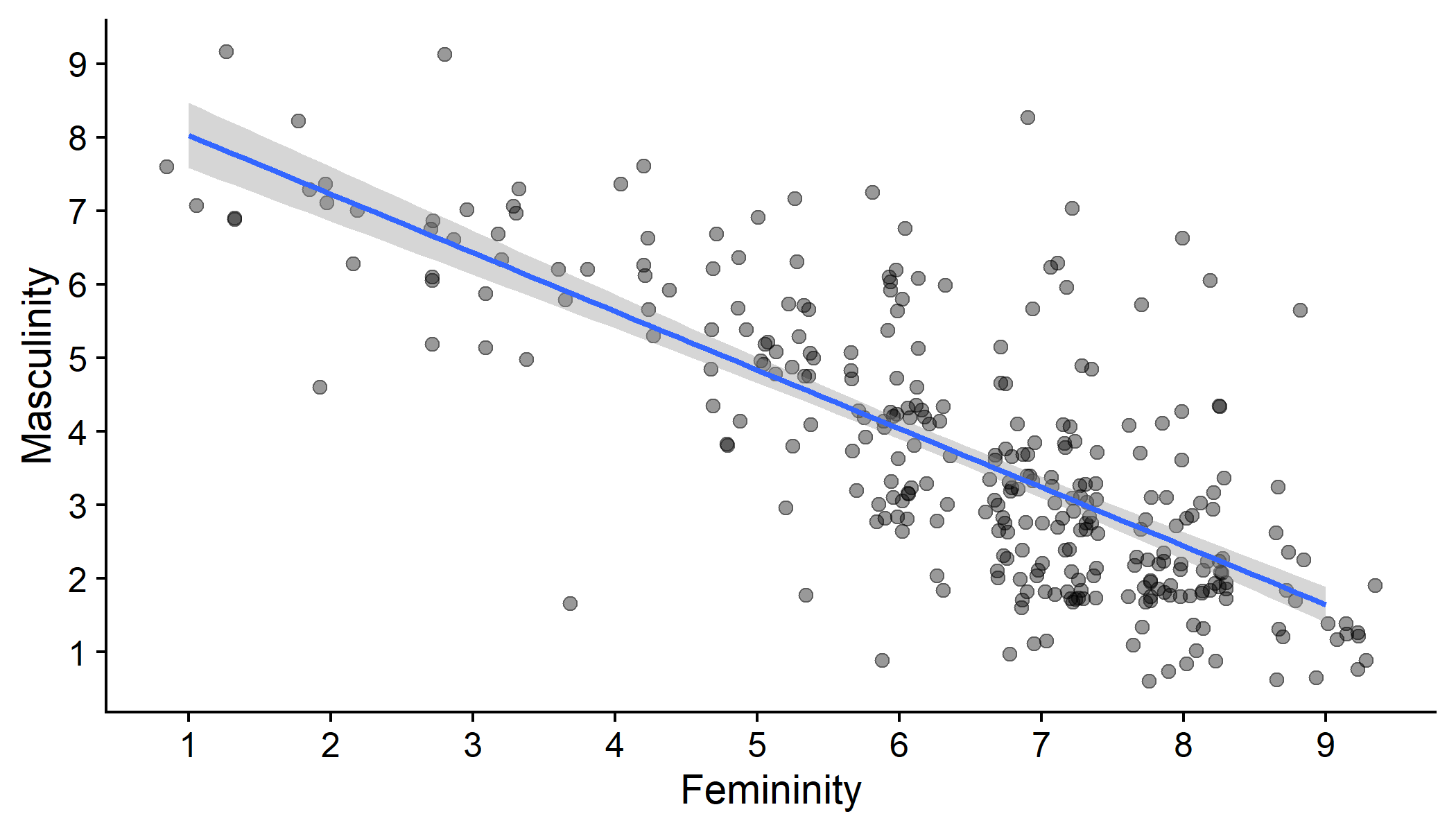
gensex %>% mutate(Gender = fct_explicit_na(Gender)) %>% ggplot(aes(x = Gender_fem_1, y = Gender_masc_1)) + geom_point(position = "jitter", size = 2, alpha = .4) + geom_smooth(method = "lm", formula = y ~ x) + scale_x_continuous(name = "Femininity", breaks = c(0:9)) + scale_y_continuous(name = "Masculinity", breaks = c(0:9)) + cowplot::theme_cowplot()
Comparing to the Model
- Someone with a femininity of 3 will have a predicted masculinity rating of 6.42
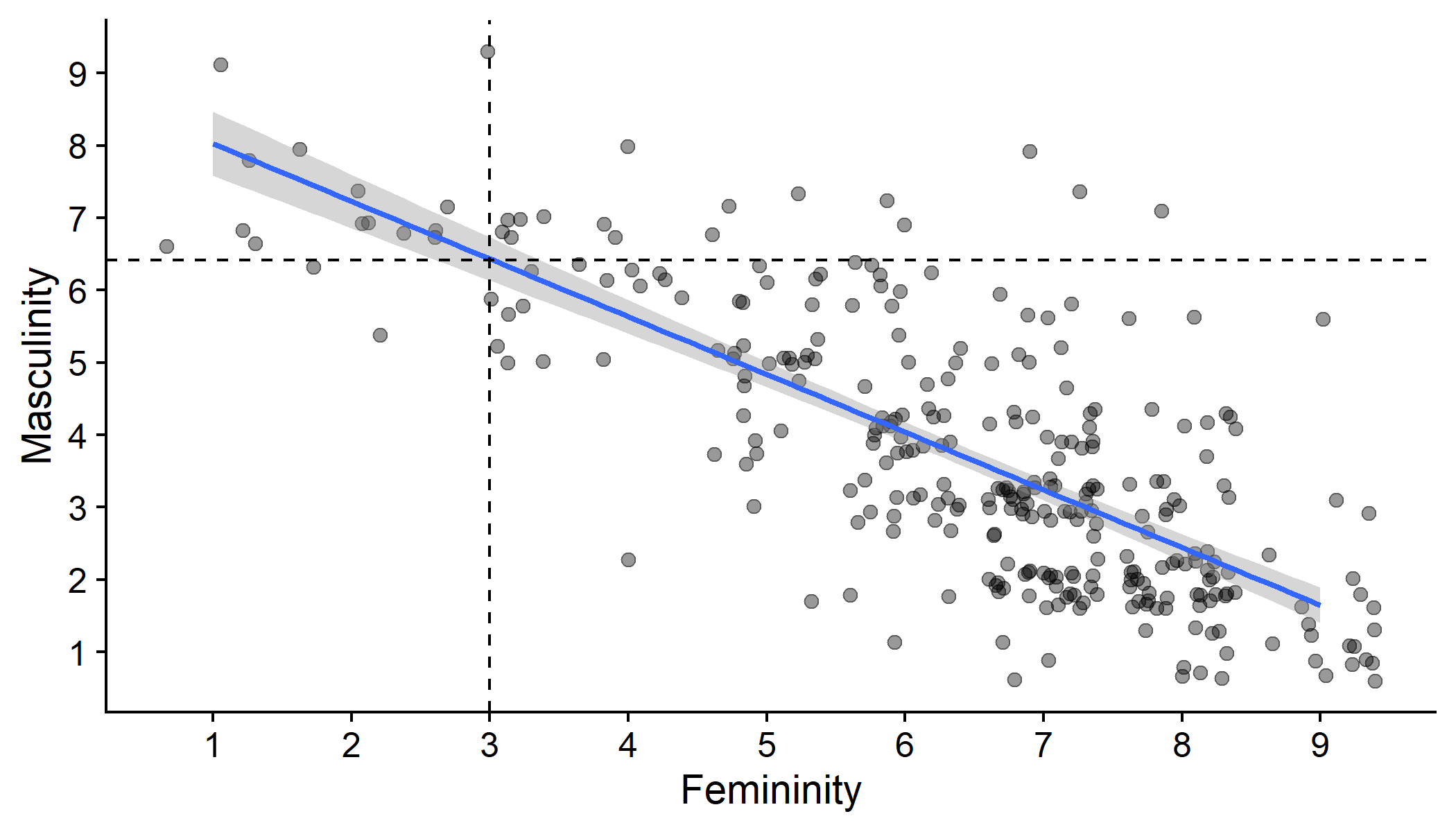
gensex %>% mutate(Gender = fct_explicit_na(Gender)) %>% ggplot(aes(x = Gender_fem_1, y = Gender_masc_1)) + geom_point(position = "jitter", size = 2, alpha = .4) + geom_smooth(method = "lm", formula = y ~ x) + geom_vline(xintercept = 3, linetype = "dashed") + geom_hline(yintercept = 6.42, linetype = "dashed") + scale_x_continuous(name = "Femininity", breaks = c(0:9)) + scale_y_continuous(name = "Masculinity", breaks = c(0:9)) + cowplot::theme_cowplot()
Summary
The linear model (LM) expresses the relationship between at least one predictor, x, and an outcome, ^y
Linear model equation: yi=b0+b1x1i+ei
Predictors can be categorical or continuous!
Most important result is the parameter b1, which expresses the change in y for each unit change in x
Used to predict the outcome for a given value of the predictor
Next week: significance and model fit

